Introduction
The prefectures of Ioannina, Greece and Gjirokaster, Albania are neighboring districts with common characteristics. Both prefectures are inhabited mostly by a rural population, while both are remotely situated in the northwestern and southeastern part of Greece and Albania, respectively.
Primary care services in rural areas of both prefectures are provided mainly by primary care physicians and nurse-midwives. In Albania, primary care services are provided by GPs. The main unit of provision of rural primary care in Albania consists of health centers1. In Greece most of the physicians providing primary care are non-specialized medicine graduates, while the rest are qualified GPs or qualified internal medicine physicians. In the Greek rural primary care setting, health care is provided in health centers, as well as in affiliated health posts2.
Inequalities in the distribution of primary care physicians are of great importance in the provision of health care3. This becomes more apparent mainly in the rural and remote areas of each country4.
The main aim of the present study was to evaluate the degree of inequality in the provision of primary care physicians in Ioannina and Gjirokaster prefectures during 2001, and to compare the inequalities in terms of relative inequality measures between the two prefectures.
Methods
Data sources
Data on the population of each village in the prefecture of Ioannina were obtained from the General Secretariat of National Statistical Service of Greece5 and represents the actual population of each village of the 2001 Census. Data concerning the rural primary care physicians per Greek Health Center and Health Post were acquired from the Health Centers' Office, General Hospital of Ioannina, Greece. Data on the population of each village in the prefecture of Gjirokaster, as well as the number of rural primary care physicians per Albanian Health Center, were acquired from the Public Health Directorate of Gjirokaster, Albania.
Variables
The main variable used in the analyses was the population per physician ratio (PPR), which represents the number of inhabitants divided by the number of physicians.
In both prefectures, for all calculations made, we used the total number of full-time working physicians providing primary care in rural areas. This included GPs, internal medicine specialists, and non-specialised graduate physicians. All other physician specialties (eg microbiologists) were excluded from the calculations of the present study. Each rural physician provides care to the population of specific villages. Therefore, we did not use geographical territories as units of division. Instead each physician was used as a unit for the calculation of the inequality indices.
Inequality indices
In order to measure the inequality in the distribution of GPs in both districts, we used relative inequality indices.
Lorenz curve
The Lorenz curve compares the distribution of a specific variable with the uniform distribution that represents equality. This equality distribution is represented by a diagonal line, and the greater the deviation of the Lorenz curve from this line, the greater the inequality (Figure 1). In order to safely compare two Lorenz curves, these curves should not cross. If the curves do not cross, then the one closest to the diagonal represents the least unequal distribution6. The cumulative proportion of the population is generally shown on the X axis, and the cumulative proportion of the health variable on the Y axis. The greater the distance from the diagonal line, the greater the inequality. In the present study the Lorenz curve was plotted using the cumulative proportion of the number of physicians in the Y axis and the cumulative proportion of the population in the X axis.
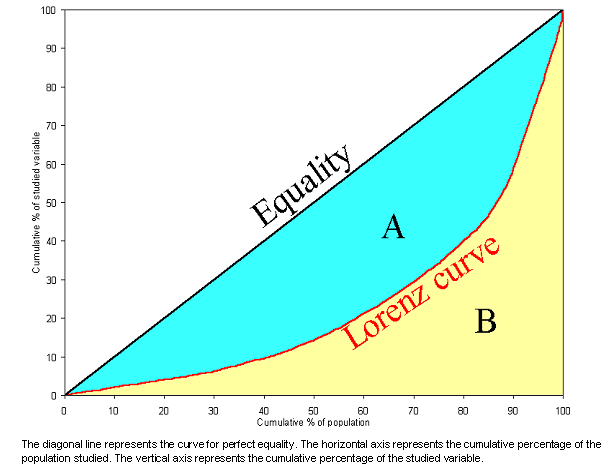
Figure 1: The Lorenz curve.
Gini coefficient
The Gini coefficient ranges from 0 to 1; 0 representing perfect equality and 1 total inequality. Geometrically, it can be derived from the Lorenz curve (Figure 1) using Formula 17:

There are different methods to calculate the Gini index; in the present study we used the formula provided by Brown8 (Formula 2).

Analyses
We first plotted the Lorenz curves and then we calculated the Gini coefficients for the distribution of physicians' workforce adjusted by population (PPR) in the two districts. These indices are mainly used in the estimation and comparison of inequalities in the distribution of income and welfare, but they were also used in the estimation of inequalities in health3,7-12. Lorenz curves were plotted using the Microsoft EXCEL 2000 for Windows. Gini coefficients and standard deviations, were calculated using the software 'DAD: a software for Distributive Analysis/Analyse Distributive', which was developed specifically for the calculation of inequality indices (Duclos J-Y, Araar A, Forten C. DAD: A software for Distributive Analysis/Analyse Distributive. MIMAP programme, International Development Research Centre, Government of Canada and CIRPΙE, Universite Laval). The same software was also used for the comparison of the two Gini values between the two districts. We repeated the analyses after excluding some extreme values of PPR. Namely we excluded PPR values of more than 6000. We also repeated the analyses after excluding the statistically significant outliers of PPR. Outliers were calculated using the extreme studentized deviate (ESD) method, also known as Grubb's method.
The p values are two tailed and were calculated for confidence levels of 95%.
Results
In the prefecture of Ioannina, Greece, rural primary care was provided in 6 health centers and the health posts affiliated to them. These were the Health Centers of Voutsara, Delvinaki, Derviziana, Konitsa, Metsovo and Pramanta. In total 85 primary care physicians were providing primary care to the rural population in the prefecture of Ioannina. The rural population of Ioannina prefecture for 2001 was 103 876. The PPR for the whole prefecture was 1222. The lowest PPR, which corresponds to better health provision, was 205, while the highest, corresponding to worse health provision was 8166 (Table 1). In the case of Gjirokaster prefecture, Albania, there were 11 rural health centers. In all, 18 physicians were providing primary care to 42 777 inhabitants, with a PPR of 2376 for the whole prefecture. The lowest PPR was 1323, while the highest was 4546 inhabitants per physician (Table 2).
Table 1: Population per physician ratio by health center in the prefecture of Ioannina, Greece, for 2001

Table 2: Population per physician ratio by health center in the prefecture of Gjirokaster, Albania, for 2001

The Lorenz curves concerning the distribution of primary care physicians in the two neighboring districts are seen in Figure 2. Because the two curves do not intersect we can assume with certainty that primary care physicians in the prefecture of Ioannina were more unevenly distributed than those in the prefecture of Gjirokaster: the curve representing the latter distribution is closer to the diagonal of equality. The same results are derived when Gini coefficients are used. The Gini coefficient for the distribution of primary care physicians in Ioannina prefecture was 0.489 (SD = 0.045, lower bound = 0.401, upper bound = 0.578), while that of the Gjirokaster prefecture was 0.186 (SD = 0.034, lower bound = 0.119, upper bound = 0.254). The difference between the two Gini indices was 0.303 (p <0.001).

Figure 2: Lorenz curves of the distribution of primary care physicians in the prefectures of Ioannina, Greece and Gjirokaster, Albania, for 2001.
After excluding from the analyses the three extreme values from the Voutsara area, the Gini coefficient for Ioannina prefecture was 0.383 (SD = 0.031, lower bound = 0.323, upper bound = 0.443). In this case the difference between the Gini index for Ioannina and Gjyrokaster was 0.197 (p <0.001). After excluding the statistically significant outlier of PPR (PPR = 8,166; p <0.05) the Gini coefficient for Ioannina prefecture was 0.443 (SD = 0.044, lower bound = 0.357, upper bound = 0.529), while the corresponding difference was in Gini coefficients was 0.257 (p <0.001).
Discussion
Primary care physicians were unevenly distributed in both sides of the border. The inequality in the distribution of primary care physicians was significantly higher in the prefecture of Ioannina, Greece than in the prefecture of Gjirokaster, Albania. This became apparent after comparing the Lorenz curves, as well as the Gini coefficients.
Because, in both prefectures, primary care physicians are state employees, it seems the main reason for the inequality observed is primary care health planning and not 'market' choice. This probably means that Albanian health workforce planning in this prefecture has been more effective, compared with the Greek planning. Greek policy makers, and Albanian to a lesser extend, should focus on re-planning of primary care workforce distribution according to population density and population needs.
With the present study we intended to investigate the degree of inequality in the distribution of rural primary care physicians in two rural and remote prefectures on the Greek-Albanian border, and compare the inequality through the use of relative inequality indices (Lorenz curve and Gini coefficient). This comparison was possible because the prefectures have many similarities; they are neighboring prefectures, the rural primary care systems in both countries are similar, the access to rural health care units is almost the same because both are mountainous prefectures, and they present a common diagnosis panorama13.
There are, however, several issues that should be taken into consideration. Lorenz curve is a visual method used for the comparison of inequality. However, it is not always an accurate method of yielding the exact differences. In our case, because the two curves did not 'cross', the comparison leads to confident results of dominance of one curve over the other6. Furthermore, for reasons of validity and accuracy we also used the Gini coefficients, which resulted to the same direction in the comparison of the two inequalities. One other issue is that, in the present study, the number of physicians was adjusted for population (PPR), which represents a common indicator of health care provision4,9,11,12. The PPR is an indicator of health services provision, but a more accurate reflection of the true conditions of primary care provision would be obtained if the calculations were made after adjustment for population health need3. There was no need of adjusting for whole time equivalent in the analyses because, in both prefectures, primary care physicians' workforce comprised only full-time working state employees.
One other issue contributing to the observed inequality is the fact that some areas within the studied prefectures appear to be excessively under-served. We tried to address this issue by repeating the analyses after excluding these areas. The difference in the inequality in the distribution of physicians in the two prefectures was lower in this case, but still statistically significant. The results remained robust even after excluding from the analyses the statistically significant outliers of PPR. From a statistical point of view the exclusion of some extreme PPR values from the analyses could be necessary for robust results. However, contrary to that, from a policy point of view, extreme values are the main reason for the observed inequalities. Therefore, it is of great importance to get to the heart of the problem and eliminate the inequalities by further supplying the underserved areas.
It would be valuable to adjust for mortality or morbidity patterns in these areas in order to eliminate any potential bias of significant differences explaining the distribution of physicians in the two areas. However, this was not possible in the present study, because there was no data available at village level for either prefecture. Further investigations could be performed using a need adjusted index instead of PPR14. For this purpose, the number of physicians could be adjusted for other parameters such as mortality, chronic disease morbidity and limiting longstanding illness3,14. Studying the inequality patterns in districts could be aided by the use of other disciplines, such as Geographical Information Systems (GIS)15, giving a clearer picture of the situation of primary care provision in these districts.
The results of the present study could be considered by health policy researchers. It seems that human resources' density and inequality in the distribution of health manpower are both needed as indicators for a more thorough investigation of health services, especially in the case of rural and remote areas.
Furthermore, health policy makers should focus on the redistribution of health manpower towards a more equitable one, based on the results of similar studies. Moreover, the documentation of inter-country differences would prove helpful in terms of international cooperation and sharing of knowledge by policy makers, when the objective is the equality and quality of health services provision.
Acknowledgement
The authors would like to thank Professor Jean Yves Duclos from CIRPΙE, Universite Laval, Canada, who developed the DAD software, for his valuable comments on methodological aspects of the paper.
References
1. European Observatory on Health Care Systems. Health care systems in transition: Albania. (Online) 2005. Available: http://www.euro.who.int/observatory (Accessed 10 June 2005).
2. European Observatory on Health Care Systems. Health care systems in transition: Greece. (Online) 2005. Available: http://www.euro.who.int/observatory (Accessed 10 June 2005).
3. Gravelle H, Sutton M. Inequality in the geographical distribution of general practitioners in England and Wales 1974-1995. Journal of Health Services Research & Policy 2001; 6: 6-13.
4. Wilkinson D. Inequitable distribution of general practitioners in Australia: analysis by state and territory using census data. Australian Journal of Rural Health 2000; 8: 87-93.
5. General Secretariat of National Statistical Service of Greece. Actual population of Greece, 2001 census. (Online) 2005. Available: http://www.statistics.gr (Accessed 5 August 2003).
6. Torado MP. Growth, poverty and income distribution. In: Economic Development, 6th edn. Essex: Addison Wesley Longman, 1997; 137-188.
7. Pan American Health Organization (PAHO). Measuring Health Inequalities: Gini Coefficient and Concentration Index. (Online) 2001. Available: http://www.paho.org (Accessed 10 April 2001).
8. Brown M. Using Gini-style indices to evaluate the spatial patterns of health practitioners: theoretical considerations and an application based on Alberta data. Social Science & Medicine 1994; 38: 1243-1256.
9. Kobayashi Y, Takaki H. Geographic distribution of physicians in Japan. Lancet 1992; 340: 1391-1393.
10. Gravelle H, Sutton M. Trends in geographical inequalities in provision of general practitioners in England and Wales. Lancet 1998; 352: 1910.
11. Chang R-KR, Halfon N. Geographic distribution of pediatricians in the United States: An Analysis of the Fifty States and Washington, DC. Pediatricsk 1997; 100: 172-179.
12. Mantzavinis G, Theodorakis PN, Lionis C, Trell E. Geographical inequalities in the distribution of general practitioners in Sweden. Lakartidningen 2003; 100: 4294-4297.
13. Theodorakis PN. Evaluation of primary health care services quality parameters in the prefectures of Ioannina and Gjirokaster on the Greek-Albanian border. A contribution to general practice (PhD thesis). Ioannina, Greece: University of Ioannina, 2003.
14. Mantzavinis GD, Theodorakis PN, Dimoliatis I. Robin Hood Index under discussion. Australian and New Zealand Journal of Public Health 2002; 26: 79-80.
15. Kohli S, Sahlen K, Lofman O, Sivertun A, Foldevi M, Trell E, Wigertz O. Individuals living in areas with high background radon: a GIS method to identify populations at risk. Computer Methods and Programs in Biomedicine 1997; 53: 105-112.
Abstract
Introduction: Inequalities in the distribution of primary care physicians are of great importance in the provision of health care. This becomes more apparent mainly in the rural and remote areas of each country. The objective of the present study was to evaluate and compare the degree of inequality in the provision of primary care physicians in two rural and remote prefectures of neighboring countries. We studied the cases of Ioannina, Greece and Gjirokaster, Albania during 2001.
Methods: In both prefectures, for all calculations made, we used the total number of physicians providing primary care in rural areas. This includes GPs, internal medicine specialists, non-specialised graduate physicians. All other physician specialties (eg microbiologists) were excluded from the calculations of the present study. We calculated the population per physician ratio (PPR) for each health center in each prefecture. For the comparison of the inequality we used two relative inequality measures. We plotted the Lorenz curves and calculated the Gini coefficients for the distribution of physicians' workforce adjusted by population in the two districts. Finally, we calculated the difference in the inequalities in these distributions. The p values were two tailed and calculated for 95% confidence levels.
Results: The PPR for the whole prefecture of Ioannina, Greece was 1222. The lowest PPR, which corresponds to higher supply of human resources, was 205, while the highest (worst) was 8166. In the case of Gjirokaster the PPR was 2376 for the whole prefecture. The lowest PPR was 1323, while the highest was 4546 inhabitants per physician. Because the two curves do not intersect we can assume with certainty that primary care physicians in the prefecture of Ioannina were more unevenly distributed than those in the prefecture of Gjirokaster. The Gini coefficient for the distribution of primary care physicians in Ioannina was 0.489 (SD = 0.045), while that of the Gjirokaster district was 0.186 (SD = 0.034). The difference between the two Gini indices was 0.303 (p <0.001).
Conclusions: Primary care physicians in both prefectures were unevenly distributed. The inequality in the distribution of primary care physicians was significantly higher in the prefecture of Ioannina, Greece compared with that of the prefecture of Gjirokaster, Albania. Further investigations could be made using a need adjusted index instead of PPR. For this purpose, the number of physicians could be adjusted for mortality, morbidity of chronic diseases or limiting longstanding illness. Studying the inequality patterns in districts could be aided by the use of other disciplines, such as geographical information systems, giving a clearer picture of the situation of primary care provision in these districts. The results of the present study could be considered by health policy researchers. It seems that human resources' density and inequality in the distribution of health manpower are both needed as indicators for a more thorough investigation of health services, especially in the case of rural and remote areas. Furthermore, health policy makers should focus on the redistribution of the health manpower towards a more equitable situation, based on the results of similar studies. Finally, the documentation of inter-country differences would prove helpful in terms of international cooperation and sharing of knowledge by policy makers when the objective is the equality and quality of health services provision.
Key words: Albania, Gini index, Greece, inequality, Lorenz curve, physicians' distribution, rural primary care.
You might also be interested in:
2008 - Quality of life in patients with sickle cell disease in Jamaica: rural-urban differences

